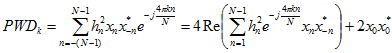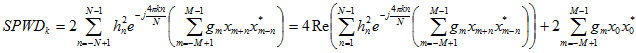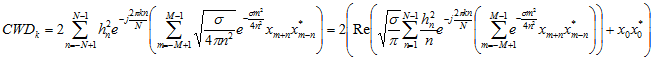CCANA
CCANA - general Cohen class analysis
A general Cohen class analysis SPAtom.
Usage:
SPU CCANA WAVE HOPSIZE ITYP FTYP ANALYTICSIGNAL MAXSIZE DTYP LSIG WSIG LSMO WSMO EPS DB AMAX AREF
Inputs:
- WAVE
- The input signal wave item (mono).
- HOPSIZE
- The distance between frames in samples.
- ITYP
- The input frame alignment (values: BEGIN, CENTER).
- FTYP
- The input filter (NONE, DOUBLESRATE, HALFBANDWIDTH, ANALYTICSIGNAL).
- MAXSIZE
- The maximum signal queue length.
- DTYP
- The Cohen class distribution type (WIGNERVILLE, CHOIWILLIAMS).
- LSIG
- The signal window length in samples.
- WSIG
- The signal window type. The following values are supported(RECTANGLE, HANNING, HAMMING).
- LSMO
- The smoothing window length in samples.
- WSMO
- DTYP=
WIGNERVILLE-> smoothing window type (RECTANGLE, HANNING, HAMMING)
- DTYP=
CHOIWILLIAMS-> smoothing window coef. sigma (0 < sigma)
- EPS
- DTYP=
WIGNERVILLE-> not used
- DTYP=
CHOIWILLIAMS-> minimum smoothing window value
- DB
- 1 if the amplitude scale is in dB, 0 otherwise. The default is 0.
- AMAX
- An amplitude value > 0. The default is 1.
- AREF
- A reference amplitude > 0. The default is 1.
Outputs:
- Y
- The amplitudes.
- DT
- The time resolution in seconds
- DF
- The frequency resolution in Hz.
- LMAX
- The maximum frame length in samples.
- I
- The number of processed frames.
- N
- The maximum number of frames.
- SR
- The sampling rate in Hz.
Function:
The SPAtom CCANA implements a Psuedo Wigner-Ville Distribution (PWD), a Smoothed Pseudo Wigner-Ville Distribution (SPWD) and a Choi-Williams Distribution (CWD).
Pseudo Wigner-Ville Distribution (PWD)
where
k - Frequency index, k = 0..N/4
hn - Symmetrical, real signal window function of length 2N-1
xn - The complex signal of length 2(N-1)+1
n - The time index (sample index), n = -(N-1)..(N-1)
N - The transformation length
Smoothed Pseudo Wigner-Ville Distribution (SPWD)
where
k - The frequency index, k = 0..N/4
hn - The symmetrical real signal window of length 2N-1
gm - The symmetrical real smoothing window of length 2M-1
xm±n - The real/complex signal of length 2(M-1)+2(N-1)+1
m - The shift index, m = -(M-1)..(M-1)
n - The time index (sample index), n = -(N-1)..(N-1)
M - The smoothing length
N - The transformation length
Choi-Williams Distribution (CWD)
where
k - The frequency index, k = 0..N/2
hn - The symmetrical real signal window of length 2N-1
s - The distribution parameter (>0)
xm±n - The real/complex signal of length 2(M-1)+2(N-1)+1
m - The shift index, m = -(M-1)..(M-1)
n - The time index (sample index), n = -(N-1)..(N-1)
M - The smoothing length
N - The transformation length.