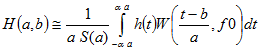MORLET
MORLET - wavelet transform
Usage:
MORLET X SP SR DF FB LB F0 ACUT TYP O FMT MAMI MAMX MPV
Inputs:
| X | input signal; length depends on lowest frequency |
| SR | sampling frequency in Hz |
| DF | frequency resolution in Hz |
| FB, LB | first and last frequency bin of wavelet analysis |
| F0, O, ACUT | wavelet parameters (see function description) |
| TYP | wavelet typ |
| FMT | output format |
| SP, MAMI,MAMX, MPV | phase locking and masking parameters; see atom SPECTRUM |
Outputs:
| WR, WI | wavelet spectrum output; depends on FMT |
| FR | vector of center frequencies |
| BW | vector or bandwidth frequencies |
| TW | vector of timewidth values |
Function:
This module computes a wavelet analysis using different types of wavelets. In S_TOOLS-STx a scaled wavelet transformation with a bounded integration interval is used:
with:
| a | frequency scaling parameter |
| b | time shift parameter |
| S(a) | amplitude scaling factor |
| a | time window width (input ACUT |
| f0 | basic frequency of wavelet function (input F0) |
The wavelet function W is defined by the inputs TYP (type of wavelet), ACUT (window width), F0 (basic frequency) and O (order). The available wavelet types and the parameters are described later in this section. The time shift parameter b is always set to the center of the input signal, because the frame shifting is performed outside the module (by the signal I/O functions).
The wavelet transform is computed for a set of discrete frequencies fI, which are defined by the inputs DF, FB (first bin) and LB (last bin):
with:
| I | frequency bin index, FB <= I <= LB |
| DF | frequency resolution in Hz |
The scaling factor S(a) is computed for each frequency fI to get the magnitude 1 for a pure sinoid with frequency fI. This scaling is performed to get a 'wavelet spectrum' that is comparable to other spectrum analysis/transformation methods.
For each input signal frame X the wavelet transform of all frequency bins fI is computed:
with:
| f0 | basic frequency of wavelet function (see wavelet table below) |
| aI | frequency scaling factor for bin I (= f0/fI) |
| tA | point of analysis, set to the center of the signal vector |
| wrI, wiI | real an imaginary part of H' at bin I; |
The values wrI and wiI are converted to different formats (see output format table) and stored in the outputs WR and WI. In addition the center frequencies (fI, output FR), the analysis bandwidths (output BW) and time window widths (output TW) of each bin are computed and stored in outputs.
The length of the input signal X (NX) should be equal to (or greater than) the longest time window. If the signal is shorter zero padding on both sides in performed.
The input SP, MAMI, MAMX and MPV are used for the phase computation and are processed in the same way as for the atom SPECTRUM. Phase locking and masking is also described in this section.
Table 15: Wavelet functions (input TYP) and parameters (inputs F0 and O){|
|-
|TYP
|wavelet W(t)
|F0, O (comments)
|-
|0
|Morlet:![]() |f0 = F0
|-
|1
|Generalized Morlet:
|f0 = F0
|-
|1
|Generalized Morlet: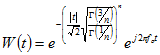 |f0 = F0n = O
|-
|2
|Laplace:
|f0 = F0n = O
|-
|2
|Laplace:![]() |f0 = F0
|-
|3
|n-th derivative Gaussian:
|f0 = F0
|-
|3
|n-th derivative Gaussian: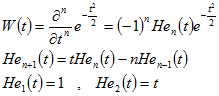 |n = F0 (integer, >=0)
|n = F0 (integer, >=0)![]() |-
|4
|Mexican Hat: special case of n-th derivative Gaussian with n equals 2
|f0 = F0
|-
|5
|Goupillaud:
|-
|4
|Mexican Hat: special case of n-th derivative Gaussian with n equals 2
|f0 = F0
|-
|5
|Goupillaud: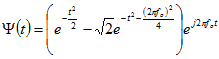 |f0 = F0
|-
|6
|Morlet II:
|f0 = F0
|-
|6
|Morlet II:![]() |f0 = F0
|}
|f0 = F0
|}
Table 16: Output formats (selected by input FMT)
| FMT | output WR | output WI |
| 0, 10 | real part: WRI = wrI | imaginary part: WII = wiI |
| 1 | energy: WRI = aI2 | phase: WII = jI |
| 2 | real part: WRI = wrI | all zero: WII = 0 |
| 3 | imaginary part: WRI = wiI | all zero: WII = 0 |
| 4 | amplitude: WRI = aI | all zero: WII = 0 |
| 5 | phase: WRI = jI | all zero: WII = 0 |
| 6 | energy: WRI = aI2 | locked phase: WII = j'I |
| 7 | amplitude (dB): WRI = 20.log10(aI) | phase: WII = jI |
| 8 | amplitude (dB): WRI = 20.log10(aI) | locked phase: WII = j'I |
| 9 | locked phase: WRI = j'I | all zero: WII = 0 |
with:
| I | bin index (FB, ..., LB) |
| wrI, wiI | real and imaginary part of the wavelet bin I |
| aI | amplitude of wavelet bin I (aI2 = wrI2 + wiI2) |
| jI, j'I | unlocked/locked phase of wavelet bin I (jI = arctan(wiI/wrI)) |